One of the core problems in modern statistics is efficiently computing complex probability distributions. Solving this problem is particularly important in Bayesian statistics, whose core principle is to frame inference about unknown variables as a calculation involving a posterior probability distribution.
Exact inference techniques such as the elimination algorithm, the message-passing algorithm, and the junction-tree algorithm involve analytically computing the posterior distribution over the variables of interest. However, in the case of large data sets and complicated posterior probability densities, exact inference algorithms favor accuracy at the cost of speed.
On the other hand, approximate inference techniques offer an efficient solution by estimating the actual posterior probability distribution. Various Markov Chain Monte Carlo (MCMC) techniques such as Metropolis-Hastings and Gibbs’ Sampling fall under this category of algorithms. Since the early 1950s, researchers have extensively studied MCMC techniques that have developed into an indispensable statistical tool for solving approximate inference in recent years. However, these traditional sampling methods are slow to converge and are not scalable.
Alternatively, another approximate inference technique named Variational Inference (VI) offers an efficient solution for tractably computing complex posterior probability distributions. The main idea of VI is to select a tractable approximation to the true posterior distribution by using a suitable metric, which is usually the Kullback–Leibler (KL) divergence. This methodology of VI re-frames the statistical inference problem into an optimization problem.
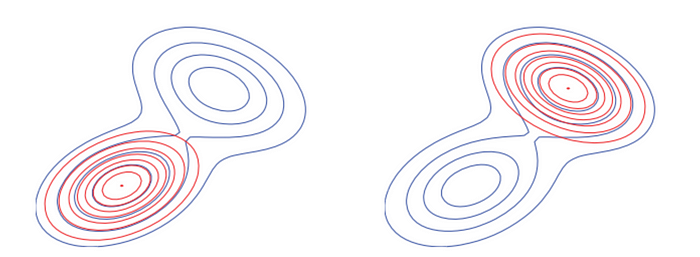
Unlike sampling-based methods, VI trades off finding a globally optimal solution with convergence. Additionally, VI often scales better and are can easily be coupled with techniques like stochastic gradient optimization, parallelization over multiple processors, and acceleration using GPUs.
Furthermore, VI enables an efficient computation of a lower bound to the observed data distribution. This lower bound is popularly referred to as the Evidence Lower BOund (ELBO). The idea is that a higher marginal likelihood is indicative of a better fit to the observed data by the chosen statistical model.
In recent years, VI techniques have gained immense popularity in statistical physics and generative modeling, especially for image generation. Additionally, machine learning problems like anomaly detection, time series estimation, language modeling, dimensionality reduction, and unsupervised representation learning have all used VI in one form or the other.
Members from the Sertis AI research team, namely Ankush Ganguly and Samuel W. F. Earp, studied VI and its applications and summarized their findings in a paper. The researchers authored the paper intending to provide an intuitive explanation of the mathematical foundations for VI. The paper describes the problem statement for VI, introduces the idea of using KL-divergence as the metric for the VI optimization process, and discusses the concept of ELBO and its importance. Additionally, the paper demonstrates the application of VI to a mixture of Gaussians. Furthermore, it extends on a few practical applications of VI in deep learning and computer vision.
Read the full research at: https://arxiv.org/abs/2108.13083
Written by: Sertis Vision Lab
Originally published at https://www.sertiscorp.com/
